Carte blancheLes mathématiques, un grand défi de cette pandémie

Voilà des questions que se sont sans doute posées de nombreux habitants du Grand-Duché, soucieux non seulement des restrictions liées aux mesures imposées, mais aussi bien sûr des conséquences financières. Alors que ces préoccupations et l’aspiration à un retour à la normale apparaissent tout à fait légitimes, la critique „les mesures prises ne servent à rien“ ne l’est pas. Depuis mars, une avalanche de nombres s’abat quotidiennement sur nous. Sans compréhension mathématique basique, il est difficile, voire impossible de s’y retrouver, et d’en extraire les informations utiles. Quoi, les mathématiques, ce domaine difficile et craint par tant de gens? Cette science dont certains sont parfois fiers d’affirmer qu’ils n’y ont jamais rien compris, et dont on se demande parfois à quoi elle sert dans la vie? Oui, exactement, ces mathématiques-là, qui sont d’ailleurs omniprésentes dans notre vie quotidienne! A travers cet article, nous espérons montrer comment une meilleure connaissance de notions mathématiques fondamentales, particulièrement de notions statistiques, permettrait de mieux comprendre l’évolution du virus et, par la même occasion, les mesures de confinement et déconfinement adoptées par le gouvernement.

Revenons-en aux 190 nouvelles infections détectées le 31 mars 2020, portant le nombre total d’infectés à 2178. On ne peut pas interpréter ce nombre sans connaître le contexte spécifique dans lequel il est obtenu. Si la veille, à savoir le 30 mars le nombre total d’infections détectées avait été de 190, alors très clairement 190 nouvelles infections aurait été une croissance énorme, correspondant à un doublement des cas positifs d’un jour à l’autre. Pareille évolution montrerait les conséquences néfastes d’une croissance incontrôlable, développée dans le paragraphe ci-dessous „La fameuse croissance exponentielle et le temps de doublement“. Or il faut bien voir qu’au 30 mars, le Luxembourg comptait 1.988 infections détectées – le dépassement du seuil des 2.000 était donc quasi certain. Mais il y a plus frappant que cela.

Comparées à 1.988 infections détectées, 190 nouvelles infections représentent une croissance de 9,6% (= (2.178-1.988) / 1.988). Mais 14 jours plus tôt, quand on est passé de 140 à 203 infections détectées, cela représentait une croissance bien supérieure, à savoir 45% (= (203-140) / 140)! En regardant les nombres dans leur contexte, c’est-à-dire en analysant les taux de croissance au lieu des nombres totaux (qui, eux, sont plutôt importants pour la planification de la prise en charge hospitalière), on se rend bien mieux compte de la réalité de la situation. Et on comprend que oui, le confinement avec ses mesures strictes a bel et bien fait son effet, comme le montre le graphique ci-dessous.

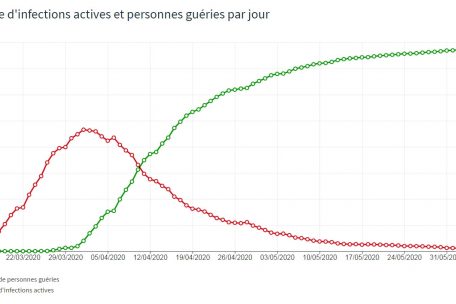
Le Luxembourg est actuellement en phase de déconfinement. Le pays peut se le permettre, vu le nombre restreint de nouveaux infectés, tout en gardant bien sûr en tête qu’il faut rester prudent et suivre les règles afin d’éviter une seconde vague.

Le petit raisonnement précédent illustre l’essence de notre message: il est capital, pour tout un chacun, d’avoir une compréhension plus profonde des nombres qui nous racontent des histoires. Il est par exemple bien utile d’avoir une idée claire sur la différence entre la notion de moyenne et la notion de médiane. La première notion, qui représente la somme des données divisée par leur nombre, est très sensible aux valeurs extrêmes: elle peut se retrouver fortement changée par une valeur très différente du reste. Tout le contraire de la seconde notion, celle de médiane, qui est la valeur qui partage l’ensemble des données rangées par ordre croissant en deux sous-ensembles de même effectif, et qui par nature même est complètement insensible aux valeurs extrêmes.

En guise d’illustration, supposons que 5 personnes âgées de 84, 85, 87, 88 et 41 ans soient mortes à la suite d’une infection Covid-19. L’âge médian est de 85 ans, tandis que l’âge moyen correspond à 77 ans. Lire la moyenne d’âge des personnes mortes du Covid-19 n’est donc absolument pas la même chose que lire l’âge médian. Et sans connaissance préalable, on risque d’en tirer de fausses conclusions, comme par exemple d’estimer que l’âge des patients décédés se situe plus proche de 75 que de 85 ans. Pour un médecin, une différence de 10 ans pour une cohorte de patients souffrant d’une maladie contagieuse comme le Covid-19 représente une différence énorme pour leur prise en charge concernant les médicaments et les traitements.

Les premières semaines de l’épidémie, on parlait d’une croissance exponentielle du nombre d’infectés détectés, déclenchant une vague incontrôlable de patients dans les unités de soins intensifs des établissements hospitaliers, ce à quoi aucun système sanitaire ne peut se préparer à court terme. La croissance exponentielle peut donner une fausse sensation de contrôle de la situation. Car au début, elle peut afficher des nombres très modérés. Prenons une infection avec une croissance quotidienne de facteur 2 (autrement dit, chaque jour le nombre d’infectés double par rapport à la veille). Si on commence avec une personne infectée (le fameux patient zéro) le premier jour, on en aura 2 le deuxième jour, puis 4 le troisième le jour, puis 8 le quatrième jour, puis 16, puis 32, puis 64, puis 128, … et au bout de seulement 11 jours, on en est déjà à plus de 1.000 infectés!

Ces nombres montrent bien pourquoi les experts n’ont cessé de dire qu’il fallait absolument stopper la croissance exponentielle. Ils soulignent également à quel point il est crucial d’être capable de comprendre ce type de croissance: un sentiment de sécurité au début peut presque d’un jour à l’autre se transformer en une sensation de panique devant les lourdes conséquences dues à une réaction forcément trop lente car dépassée par les événements.

L’exemple de croissance exponentielle que nous venons de discuter nous amène directement au concept de temps de doublement, qui était de 1 jour dans notre exemple fictif. Ce temps est défini comme la durée qui s’écoule jusqu’à ce qu’une quantité d’intérêt, ici le nombre d’infectés détectés, double. Dans le cas du Covid-19, un jour ne serait bien sûr pas acceptable. Par contre, un temps de doublement de l’ordre de 18 jours est tolérable. Le nombre total d’infectés restera le même, mais le temps jusqu’à l’atteindre diffèrera énormément et permettra au système sanitaire de faire face. Car les personnes infectées qui auront besoin de soins intensifs ne se rendront pas à l’hôpital en même temps, mais sur une période de temps bien plus étalée (pendant laquelle, on l’espère, un vaccin ou au moins un médicament efficace pourrait aussi être développé). Il s’agit là précisément de la stratégie „Flatten the curve“.

Même si la probabilité de décéder du Covid-19 est relativement faible au niveau individuel, le bilan humain à l’échelle d’une population entière peut être important, comme les images de Bergamo en Lombardie nous l’ont malheureusement montré. Sans mesures strictes, le nombre de morts cumulés du Covid-19 serait bien plus important au Luxembourg. Il est bon dans ce contexte de jeter un coup d’œil à la stratégie suivie par les Suédois, qui ont suivi une approche tout à fait différente de la nôtre. Si le Luxembourg avait le même nombre de morts par rapport à la taille de sa population (626.108 habitants selon le Statec, janvier 2020) que la Suède, nous aurions eu plus de 260 au lieu de 110 morts en date du 27 mai 2020. Nous passons donc des calculs mathématiques à des questions d’éthique que la politique doit trancher en connaissance de cause.

Une grande question dans le débat actuel est le nombre réel d’infectés, et pas seulement l’ensemble des personnes détectées positives. Il s’agit ici de connaître la prévalence du virus dans la population. L’étude CON-VINCE, mise sur pied par la Task Force Research Luxembourg Covid-19, est précisément destinée à nous fournir cette information importante. Pour cela, une étape cruciale est de réunir un échantillon représentatif, c’est-à-dire un échantillon de plus de 1.800 personnes adultes choisies de telle façon à ce qu’elles représentent une sorte de population miniature de la population totale du Luxembourg, en termes de structure d’âge, de sexe et de localisation géographique.

L’idée ici est exactement la même que lors de sondages politiques: à partir des résultats d’un tel sondage, on cherche à estimer combien de votes un tel parti obtiendrait dans l’ensemble de la population lors des prochaines élections. Les résultats que nous lisons dans les journaux suite aux sondages sont typiquement des intervalles du type [10,7%, 12,3%] avec 5% de marge d’erreur, et il en sera de même pour l’étude de prévalence: on trouverait par exemple que le virus a atteint [1,9%, 2,5%] (nombres fictifs) de la population avec 95% de confiance.

Ces intervalles sont bien connus en statistique et s’appellent intervalles de confiance. Ils indiquent que la vraie valeur inconnue (popularité du parti/prévalence du virus dans l’ensemble de la population) se trouve dans cet intervalle avec une marge d’erreur de 5%, ce qui signifie que 95 sur 100 sondages produiront un intervalle qui contiendra la vraie valeur (bien sûr les 95% peuvent être remplacés par n’importe quel pourcentage souhaité, ce qui changera l’intervalle par conséquent). Ce résultat permet donc de quantifier l’incertitude due au fait que, dans les deux cas, on ne considère qu’un échantillon de l’ensemble de la population, et que l’estimation est donc nécessairement entachée d’erreurs. Ces intervalles de confiance sont obtenus par des outils issus de la statistique mathématique que nous n’allons pas exposer ici, notre but ayant été d’expliquer le concept d’intervalles de confiance afin d’en simplifier la compréhension.

Nous voulons expressément souligner l’importance d’un échantillon représentatif. Si cet échantillon est bien choisi, il permet de tirer les bonnes conclusions sans nécessiter une connaissance sur l’ensemble de la population. Un bon exemple en sont les élections américaines de 2012 où le statisticien Nate Silver a su prédire correctement le vainqueur dans chacun des 50 États et ainsi la victoire de Barack Obama sur Mitt Romney. En guise de mauvais exemple, les instituts de sondages se sont lourdement trompés dans les élections françaises de 2002 où ils n’ont pas vu venir l’arrivée de Jean-Marie Le Pen au second tour, pronostiquant un second tour Jacques Chirac vs Lionel Jospin.

Selon le journaliste français Emmanuel Kessler, cela est dû à des échantillons insuffisamment représentatifs: „une frange de la population n’a pas été interrogée: il s’agit de la catégorie la moins diplômée, la plus populaire, la moins cultivée. Cet élément majeur explique, sans doute, les erreurs. „L’impact de l’étude CON-VINCE est donc intimement lié à la stratégie de sélection d’individus; si ceux-là représentent bien la population du Luxembourg (ou les différents contingents dont parle la politique) et que les données récoltées sont fiables, alors la prévalence avec ses marges d’erreur peut être bien quantifiée et nous fournir les informations nécessaires à un meilleur contrôle de la situation.

La théorie des probabilités et la statistique sont les domaines mathématiques qui étudient l’aléatoire et quantifient les incertitudes. Nous venons de discuter ci-dessus le concept d’intervalle de confiance, qui en est un bon exemple: quantifier l’incertitude, c’est dire qu’avec 90, 95 ou 99%, nous sommes sûrs que la vraie valeur inconnue se trouve dans un certain intervalle. Certaines situations aléatoires sont faciles à comprendre et donc à quantifier, comme par exemple le lancer d’une pièce de monnaie: avec 50% de chance elle tombera sur pile, et avec 50% sur face. Le résultat d’un lancer reste bien sûr tout à fait aléatoire, mais nous sommes néanmoins en mesure de décrire mathématiquement notre incertitude.

La recherche actuelle en théorie des probabilités et en statistique s’occupe évidemment de situations beaucoup plus compliquées, comme par exemple prédire l’état de santé d’une personne sur la base de son profil bio-moléculaire, qui comporte des milliers de variables comme les expressions génétiques de l’ADN. Cela passe par la création de nouveaux outils mathématiques toujours plus évolués, même si fondamentalement l’idée reste la même: comprendre, décrire et quantifier l’aléatoire, voire l’incertitude. Dans une situation comme la présente pandémie, il est extrêmement difficile de prédire quand le virus s’arrêtera, ou comment le nombre d’infectés se développera maintenant que les mesures du confinement sont successivement levées, ou encore quel sera l’impact de la réouverture du secteur Horeca.

Nous sommes loin d’avoir des certitudes. Il est cependant possible, grâce au développement de modèles mathématiques représentant au mieux possible notre population et ses habitudes, de simuler un grand nombre de fois l’avenir des semaines qui viennent. Grâce à ces nombreuses simulations, il est possible de prédire le scénario le plus vraisemblable, ainsi qu’un scénario optimiste et un scénario pessimiste. Mais rappelons-le encore une fois: tout scénario est aléatoire, vu que nul ne connaît le futur avec certitude. Ceci étant, les hypothèses qui alimentent les différents scénarios permettent de préparer le futur. Ce sont ces scénarios-là que les chercheurs de la Task Force Research Luxembourg Covid-19 sont constamment en train de perfectionner et qu’ils présentent aux divers ministères afin de les soutenir dans leurs prises de décisions.

Avec cet article, nous espérons avoir pu éclaircir certaines notions statistiques liées à la pandémie actuelle, et avoir montré l’utilité et peut-être aussi la beauté des mathématiques. Notre ambition est d’impulser un changement dans la manière de penser, à savoir changer la peur devant cette matière en un intérêt légitime. Nous souhaitons surtout encourager les jeunes pour qui les maths joueront un rôle encore plus primordial que pour les anciennes générations, suite aux avancées technologiques d’un monde digital mais également au vu des sujets actuels et futurs comme le changement climatique ou un autre nouveau virus. Apprendre à comprendre des phénomènes inconnus devient plus important que de savoir apprendre des phénomènes connus. Ce défi demande aussi une évolution de la pédagogie, sur comment enseigner les mathématiques. Afin de donner envie de découvrir le pourquoi au lieu de répéter le comment.

*Les auteurs remercient Yannick Baraud et Giovanni Peccati pour des échanges fructueux et des remarques qui ont contribué à la lisibilité de l’article.

Prof. Dr Christophe Ley, Département de Mathématiques appliquées, d’Informatique et de Statistique, Université de Gand

Prof. Dr Ivan Nourdin, Département de Mathématiques, Université du Luxembourg

Dipl-Ing, M.B.A. Pierre Mangers, MANGHINI Consulting – CEO and Business Owner